I. Purpose:

    In this lab we will apply the Bernoulli Theorem to the flow of water through a tapering circular pipe (a venturi meter).We will investigate how energy is conserved from one point to another in some types offlow and how energy is dissipated (that is, not conserved) in other conditions.
 

II. Equipment:

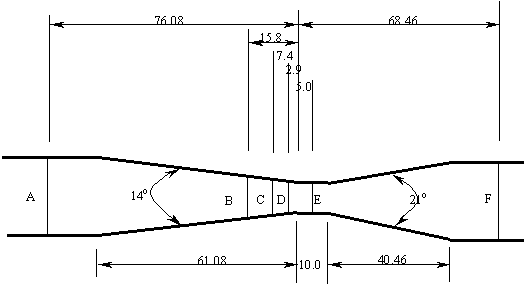
Procedure:

2.Turn on the feed water and carefully fill the manometer tubes with water to discharge all pockets of air from the system and ensure all connecting pipes are free from air.

3.Carefully adjusting the inlet feed and the flow control valve to establish the combination of flow rate and system pressure that will give the largest convenient difference between the highest and lowest manometer levels.

4.Record the scale reading of each manometer level into the Column (5) (Pressure Head).

5.Take three sets of readings of volume and time of water to find the flow rate using the volumetric tank. And find the average flow rate.

6.Insert the probe at the end of the parallel position of the duct, and then move it into the tapered portion 1cm at a time. Record its manometer scale reading in Column 7 (Stagnation Pressure Head).

III. Data Recording and Calculation:

Average Flow Rate:Q_avg = __________

Venturi Meter Reading and Calculation:
 

Mano-meter  Tube	Diameter (mm)	Velocity V=Q/A (mm/s)	Vel Head V2/2g (mm)	Pres Head h=p/g (mm)	Calc Total Head V2/2g+h (mm)	Stagnation Pres Head Hstag (mm)	% Difference Hcalc-Hstag	% of  original  total head
A	25.0							100%
B	13.9
C	11.8
D	10.7
E throat	10.0
F	25.0

Discussion:

2.Comment on the validity of Bernoulli’s equation for the system tested on the different flow sections (convergent vs divergent).